Marcelo Siqueira’s Web Spot





Siqueira, M., Latecki, L. J., Tustison, N., Gallier, J., Gee, J.
“Topological repairing of 3d digital images”,
Journal of Mathematical Imaging and Vision, 30(3), March 2008, p.249-274.
Abstract:
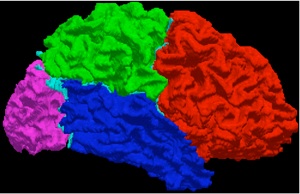
We present here a new randomized algorithm for repairing the topology of objects represented by 3D binary digital images. By "repairing the topology", we mean a systematic way of modifying a given binary image in order to produce a similar binary image which is guaranteed to be well-composed. A 3D binary digital image is said to be well-composed if, and only if, the square faces shared by background and foreground voxels form a 2D manifold. Well-composed images enjoy some special properties which can make such images very desirable in practical applications. For instance, well-known algorithms for extracting surfaces from and thinning binary images can be simplified and optimized for speed if the input image is assumed to be well-composed. Furthermore, some algorithms for computing surface curvature and extracting adaptive triangulated surfaces, directly from the binary data, can only be applied to well-composed images. Finally, we introduce an extension of the aforementioned algorithm to repairing 3D digital multivalued images. Such an algorithm finds application in repairing segmented images resulting from multi-object segmentations of other 3D digital multivalued images.
Paper (PDF)
References (BibTeX)

Stelldinger, P., Latecki, L. J., Siqueira, M.
“Topological equivalence between a 3d object and the reconstruction of its digital image”,
IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(1), January 2007, p. 126-140.
Abstract:
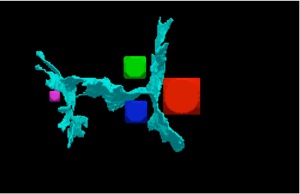
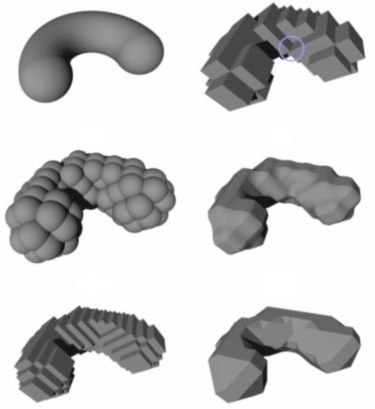
Digitization is not as easy as it looks. If one digitizes a 3D object even with a dense sampling grid, the reconstructed digital object may have topological distortions and, in general, there exists no upper bound for the Hausdorff distance. This explains why so far no algorithm has been known which guarantees topology preservation. However, as we will show, it is possible to repair the obtained digital image in a locally bounded way so that it is homeomorphic and close to the 3D object. The resulting digital object is always well-composed, which has nice implications for a lot of image analysis problems. Moreover, we will show that the surface of the original object is homeomorphic to the result of the marching cubes algorithm. This is really surprising since it means that the well-known topological problems of the marching cubes reconstruction simply do not occur for digital images of r-regular objects. Based on the trilinear interpolation, we also construct a smooth isosurface from the digital image that has the same topology as the original surface. Finally, we give a surprisingly simple topology preserving reconstruction method by using overlapping balls instead of cubical voxels. This is the first approach of digitizing 3D objects which guarantees topology preservation and gives an upper bound for the geometric distortion. Since the output can be chosen as a pure voxel presentation, a union of balls, a reconstruction by trilinear interpolation, a smooth isosurface, or the piecewise linear marching cubes surface, the results are directly applicable to a huge class of image analysis algorithms. Moreover, we show how one can efficiently estimate the volume and the surface area of 3D objects by looking at their digitizations. Measuring volume and surface area of digital objects are important problems in 3D image analysis. Good estimators should be multigrid convergent, i.e., the error goes to zero with increasing sampling density. We will show that every presented reconstruction method can be used for volume estimation and we will give a solution for the much more difficult problem of multigrid-convergent surface area estimation. Our solution is based on simple counting of voxels and we are the first to be able to give absolute bounds for the surface area.


Paper (PDF)
References (BibTeX)
Tustison, N., Avants, B., Siqueira, M., Gee, J.
“Topologically well-composedness and glamorous glue: a digital gluing algorithm for topologically constrained front propagation”,
IEEE Transactions on Image Processing (to appear)
Abstract:
We propose a new approach to front propagation algorithms based on a topological variant of well-composedness which contrasts with previous methods based on simple point detection. This provides for a theoretical justification, based on the digital Jordan separation theorem, for digitally gluing evolved well-composed objects separated by well-composed curves or surfaces. Additionally, our framework can be extended to more relaxed topologically constrained algorithms based on multi-simple points. For both methods this framework has the additional benefit of obviating the requirement for both a user-specified connectivity and a topologically-consistent marching cubes/squares algorithm in meshing the resulting segmentation.
Paper (PDF)
References (BibTeX)