Marcelo Siqueira’s Web Spot




Siqueira, M., Xu, D., Nonato, L. G., Morera, D. M., Gallier, J., Velho, L.
“A new construction of smooth surfaces from triangle meshes using parametric pseudo-manifolds”,
Computer & Graphics, 33(3), June 2009, p. 331-340.
(Special Issue of the IEEE International Conference on Shape Modeling and Applications 2009)
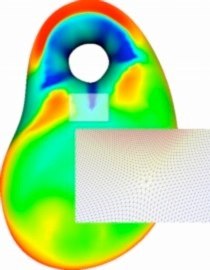
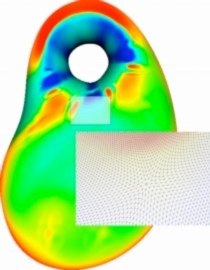
Abstract:
We introduce a new manifold-based construction for fitting a smooth surface to a triangle mesh of arbitrary topology. Our construction combines in novel ways most of the best features of previous constructions and, thus, it fills the gap left by them. We also introduce a theoretical framework that provides a sound justification for the correctness of our construction. Finally, we demonstrate the effectiveness of our manifold-based construction with a few concrete examples.
Paper (PDF)
References (BibTeX)

Castelo Filho, A., Nonato, L. G., Siqueira, M., Minghim R., Tavares, G.
“The J1a triangulation: an adaptive triangulation in any dimension”,
Computer & Graphics, 30(5), October 2006, p.737-753.
Abstract:
Spatial sampling methods have acquired great popularity due to the number of applications that need to triangulate portions of space in various dimensions. One limitation of the current techniques is the handling of the final models, which are large, complex and need to register neighborhood relationships explicitly. Additionally, most techniques are limited to Euclidean bi-dimensional or tri-dimensional spaces and many do not handle adaptive refinement well. This work presents a novel method for spatial decomposition based on simplicial meshes (the J1a triangulation) that is generally defined for Euclidean spaces of any dimension and is intrinsically adaptive. Additionally, it offers algebraic mechanisms for the decomposition itself and for indexing of neighbors that allow to recover all the information on the resulting mesh via a set of rules. With these mechanisms it is possible to save storage space by calculating the needed information instead of storing it.
Paper (PDF)
References (BibTeX)
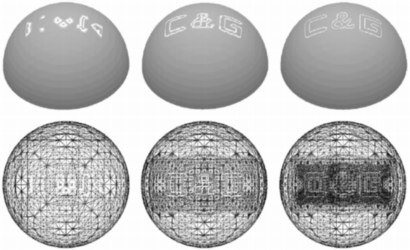

Gallier, J., Xu, D., Siqueira, M.
“Parametric pseudo-manifolds”,
Differential Geometry and Its Applications, 30(6), December, 2012, p. 702-736.
Abstract:
We introduce a novel and constructive definition of gluing data, and give the first rigorous proof that a universal manifold satisfying the Hausdorff condition can always be constructed from any set of gluing data. We also present a class of spaces called parametric pseudo-manifolds, which under certain conditions, are manifolds embedded in Rn and defined from sets of gluing data. We give a construction for building a set of gluing data from any simplicial surface in R3. This construction is an improvement of the construction given in [1], where the results were stated without proof. We also give a complete proof of the correctness of this construction making use of the crucial “property A.” The above results enable us to develop a methodology that explicitly yields manifolds in Rn arising in several graphics and engineering applications.
Paper (PDF)
References (BibTeX)


